"以Excel程式模擬反應速率" 修訂間的差異
(已建立頁面,內容為 "<div style="float:left;"> <font color="black" size="4">化學反應速率與反應物濃度、反應速率常數(rate constant) 、及反應級數(order)有關。藉…") |
|||
| 行 16: | 行 16: | ||
*3.1設定「時間差」(△t)及「時間軸」,設定一次反應之起始濃度[A]<sub>0</sub>(2.0M)及速率常數k(0.3s<sup>-1</sup>): | *3.1設定「時間差」(△t)及「時間軸」,設定一次反應之起始濃度[A]<sub>0</sub>(2.0M)及速率常數k(0.3s<sup>-1</sup>): | ||
| − | :::::<img style=" | + | :::::<img style="width:250px;" src='https://upload.wikimedia.org/wikipedia/commons/e/ec/%E4%BB%A5Excel%E7%A8%8B%E5%BC%8F%E6%A8%A1%E6%93%AC%E5%8F%8D%E6%87%89%E9%80%9F%E7%8E%871.png'/> |
::如圖,設△t = 0.1s,作時間軸 | ::如圖,設△t = 0.1s,作時間軸 | ||
| 行 25: | 行 25: | ||
::對於一次反應, 每經過△t時間,反應速率為: | ::對於一次反應, 每經過△t時間,反應速率為: | ||
| − | ::::<img style=" | + | ::::<img style="width:250px;" src='https://upload.wikimedia.org/wikipedia/commons/7/76/%E4%BB%A5Excel%E7%A8%8B%E5%BC%8F%E6%A8%A1%E6%93%AC%E5%8F%8D%E6%87%89%E9%80%9F%E7%8E%873.png'/> |
::因此時間t+△t時的反應物濃度為時間t的反應物濃度加上反應量k x[A]x△t : | ::因此時間t+△t時的反應物濃度為時間t的反應物濃度加上反應量k x[A]x△t : | ||
::::::[A]<sub>t+△t</sub>=[A]<sub>t</sub>+k x[A]<sub>t</sub> x△t (如下圖) | ::::::[A]<sub>t+△t</sub>=[A]<sub>t</sub>+k x[A]<sub>t</sub> x△t (如下圖) | ||
| 行 41: | 行 41: | ||
::對於n >1次反應, 每經過△t時間,反應速率為: | ::對於n >1次反應, 每經過△t時間,反應速率為: | ||
| − | ::::<img style=" | + | ::::<img style="width:250px;" src='https://upload.wikimedia.org/wikipedia/commons/8/82/%E4%BB%A5Excel%E7%A8%8B%E5%BC%8F%E6%A8%A1%E6%93%AC%E5%8F%8D%E6%87%89%E9%80%9F%E7%8E%877.png'/> |
::因此時間t+△t時的反應物濃度為時間t的反應物濃度加上反應量k x[A]x△t: | ::因此時間t+△t時的反應物濃度為時間t的反應物濃度加上反應量k x[A]x△t: | ||
:::::::[A]<sub>t+△t</sub>=[A]<sub>t</sub>+k x[A]<sub>t</sub><sup>n</sup>x△t | :::::::[A]<sub>t+△t</sub>=[A]<sub>t</sub>+k x[A]<sub>t</sub><sup>n</sup>x△t | ||
| 行 57: | 行 57: | ||
::以反應物起始濃度為操縱變因,得各次反應半衰期(秒)如下表( k=0.3 ) | ::以反應物起始濃度為操縱變因,得各次反應半衰期(秒)如下表( k=0.3 ) | ||
| − | ::<img style=" | + | ::<img style="width:250px;" src='https://upload.wikimedia.org/wikipedia/commons/3/33/%E4%BB%A5Excel%E7%A8%8B%E5%BC%8F%E6%A8%A1%E6%93%AC%E5%8F%8D%E6%87%89%E9%80%9F%E7%8E%878.png'/> |
<br><br> | <br><br> | ||
::從表中可以看出,一次反應的半衰期與反應物起始濃度無關,其他反應的半衰期則與起始濃度有關。 | ::從表中可以看出,一次反應的半衰期與反應物起始濃度無關,其他反應的半衰期則與起始濃度有關。 | ||
| 行 64: | 行 64: | ||
::以速率常數為操縱變因,反應物起始濃度為 2.0 M,得一次反應半衰期(秒)如下表 | ::以速率常數為操縱變因,反應物起始濃度為 2.0 M,得一次反應半衰期(秒)如下表 | ||
| − | ::<img style=" | + | ::<img style="width:250px;" src='https://upload.wikimedia.org/wikipedia/commons/e/ea/%E4%BB%A5Excel%E7%A8%8B%E5%BC%8F%E6%A8%A1%E6%93%AC%E5%8F%8D%E6%87%89%E9%80%9F%E7%8E%879.png'/> |
::以半衰期對速率常數作圖,兩者似乎成反比關係,再以半衰期對速率常數之倒數作圖,得到線性關係如下。 | ::以半衰期對速率常數作圖,兩者似乎成反比關係,再以半衰期對速率常數之倒數作圖,得到線性關係如下。 | ||
於 2019年6月19日 (三) 08:20 的修訂
化學反應速率與反應物濃度、反應速率常數(rate constant) 、及反應級數(order)有關。藉由Excel程式模擬反應物或產物與時間的關係,經由改變各種實驗條件,了解反應速率的內涵。
1.說明:
在學習反應速率的過程中,學習者接觸的核心概念包括反應速率常數、反應級數、逆反應等。對於一次反應,我們也介紹其「半衰期」與反應物起始濃度無關(=ln2/k)。Excel程式是學習反應速率的最佳工具,因為我們可以引入「一段極短時間」的概念,改變實驗條件進行探索,計算濃度與時間、反應速率與時間的關係。例如,我們可以紀錄反應物濃度與時間的關係,證明(只有)一次反應之半衰期與反應物起始濃度無關。當正反應和逆反應同時發生時,我們可以學習到化學平衡是「正反應速率和逆反應速率相等」的結果。
2.教學目標
利用Excel程式,改變實驗條件,包括反應物濃度、反應級數、逆反應等,讓學習者深入了解反應速率及平衡。教師可視時間多寡,使用電腦教室讓同學一次或分次自行完成Excel程式,或讓同學使用已完成的程式。
3.實驗步驟
- 3.1設定「時間差」(△t)及「時間軸」,設定一次反應之起始濃度[A]0(2.0M)及速率常數k(0.3s-1):
- 如圖,設△t = 0.1s,作時間軸
- 3.2 計算反應物濃度及反應速率
- 對於一次反應, 每經過△t時間,反應速率為:
- 因此時間t+△t時的反應物濃度為時間t的反應物濃度加上反應量k x[A]x△t :
- [A]t+△t=[A]t+k x[A]t x△t (如下圖)
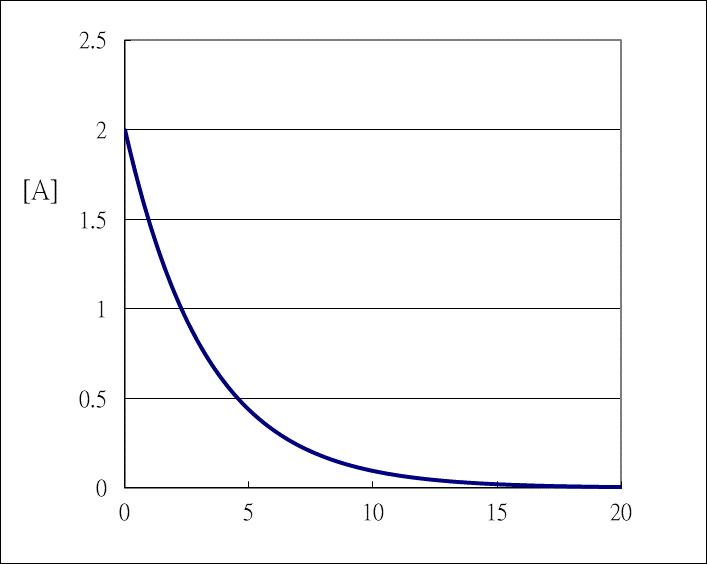
- 以反應物濃度對時間作圖如下:
- 由前述公式我們可以繪出反應速率與時間的關係如下:

- 對於n >1次反應, 每經過△t時間,反應速率為:
- 因此時間t+△t時的反應物濃度為時間t的反應物濃度加上反應量k x[A]x△t:
- [A]t+△t=[A]t+k x[A]tnx△t
- 將一次反應的程式修改(速率常數的單位不同),可得二次三次反應之濃度及反應速率關係圖。
- 3.3 半衰期
- 反應物濃度為原始濃度的二分之一所需的時間,稱為「半衰期」。試分別以反應物起始濃度、速率常數為操縱變因紀錄各反應之半衰期。
4.探索
- 4.1影響半衰期的因素
- 起始濃度:
- 以反應物起始濃度為操縱變因,得各次反應半衰期(秒)如下表( k=0.3 )
- 從表中可以看出,一次反應的半衰期與反應物起始濃度無關,其他反應的半衰期則與起始濃度有關。
- 一次反應的半衰期:
- 以速率常數為操縱變因,反應物起始濃度為 2.0 M,得一次反應半衰期(秒)如下表

- 以半衰期對速率常數作圖,兩者似乎成反比關係,再以半衰期對速率常數之倒數作圖,得到線性關係如下。
5.參考文獻
反應速率: https://en.wikipedia.org/wiki/Rate_equation
6.進階探索
- 6.1
- 一次反應之半衰期對速率常數之倒數作圖,得到線性關係。試著從這些數據計算直線的平均斜率 m,寫出半衰期與速率常數的關係式(假設截距為零)。
- 6.2
- 碳原子的同位素 14C 半衰期為 5730年,衰變是一次反應。當植物死亡後,其14C 濃度便逐年下降,我們可以藉此判斷化石或古物的年代。例如,每公克的木質化石14C 放射性是每公克現代木質的四分之一,則我們預估該化石來自11460年前的樹木。