"Rutherford與亞佛加厥常數" 修訂間的差異
| (未顯示同一使用者於中間所作的 19 次修訂) | |||
| 行 31: | 行 31: | ||
| − | == | + | ==現象說明 == |
亞佛加厥常數 | 亞佛加厥常數 | ||
| 行 44: | 行 44: | ||
<br><br> | <br><br> | ||
| − | == | + | ==探究問題 == |
*2.1 亞佛加厥常數的計算方法。 | *2.1 亞佛加厥常數的計算方法。 | ||
| 行 52: | 行 52: | ||
<br><br> | <br><br> | ||
| − | == | + | ==實作項目 == |
*3.1 閱讀關於拉賽福的實驗之說明 | *3.1 閱讀關於拉賽福的實驗之說明 | ||
| 行 65: | 行 65: | ||
::::::::::::::::::::::表一 的主要衰變路徑及其半衰期 | ::::::::::::::::::::::表一 的主要衰變路徑及其半衰期 | ||
::從鐳-226<img style="width:60px;" src='https://upload.wikimedia.org/wikipedia/commons/0/0c/%E4%BA%9E%E4%BD%9B%E5%8A%A0%E5%8E%A5%E6%95%B8-1.png'/>衰變到比較穩定的鉛-210<img style="width:50px;" src='https://upload.wikimedia.org/wikipedia/commons/2/28/%E4%BA%9E%E4%BD%9B%E5%8A%A0%E5%8E%A5%E6%95%B8-6.png'/>過程中,共有4個反應會放出α粒子,有3個反應會放出γ射線。拉賽福和蓋格將<img style="width:40px;" src='https://upload.wikimedia.org/wikipedia/commons/8/80/%E4%BA%9E%E4%BD%9B%E5%8A%A0%E5%8E%A5%E6%95%B8-7.png'/>從暴露在大量<img style="width:30px;" src='https://upload.wikimedia.org/wikipedia/commons/7/77/%E4%BA%9E%E4%BD%9B%E5%8A%A0%E5%8E%A5%E6%95%B8-8.png'/> 數小時之後的固體移開,靜置十五分鐘之後<img style="width:40px;" src='https://upload.wikimedia.org/wikipedia/commons/8/80/%E4%BA%9E%E4%BD%9B%E5%8A%A0%E5%8E%A5%E6%95%B8-7.png'/>幾乎完全衰變,所測得的α粒子幾乎都是從<img style="width:35px;" src='https://upload.wikimedia.org/wikipedia/commons/1/19/%E4%BA%9E%E4%BD%9B%E5%8A%A0%E5%8E%A5%E6%95%B8-9.png'/>的β衰變後立即由<img style="width:40px;" src='https://upload.wikimedia.org/wikipedia/commons/8/80/%E4%BA%9E%E4%BD%9B%E5%8A%A0%E5%8E%A5%E6%95%B8-7.png'/>產生。實驗測量10分鐘內衰變的α粒子數,並同時在上圖的垂直方向以另一個相似的偵測器測量樣品的γ射線強度。儀器只能量到能量較高的γ射線,由<img style="width:40px;" src='https://upload.wikimedia.org/wikipedia/commons/8/80/%E4%BA%9E%E4%BD%9B%E5%8A%A0%E5%8E%A5%E6%95%B8-7.png'/>產生的γ射線。將測量得到的γ射線強度與處於「放射性平衡」(radioactive equilibrium)的<img style="width:60px;" src='https://upload.wikimedia.org/wikipedia/commons/0/0c/%E4%BA%9E%E4%BD%9B%E5%8A%A0%E5%8E%A5%E6%95%B8-1.png'/>標準品的γ射線強度作比較,推算出樣本的相對<img style="width:60px;" src='https://upload.wikimedia.org/wikipedia/commons/0/0c/%E4%BA%9E%E4%BD%9B%E5%8A%A0%E5%8E%A5%E6%95%B8-1.png'/>質量,再算出每單位時間單位質量釋放的α粒子數。 | ::從鐳-226<img style="width:60px;" src='https://upload.wikimedia.org/wikipedia/commons/0/0c/%E4%BA%9E%E4%BD%9B%E5%8A%A0%E5%8E%A5%E6%95%B8-1.png'/>衰變到比較穩定的鉛-210<img style="width:50px;" src='https://upload.wikimedia.org/wikipedia/commons/2/28/%E4%BA%9E%E4%BD%9B%E5%8A%A0%E5%8E%A5%E6%95%B8-6.png'/>過程中,共有4個反應會放出α粒子,有3個反應會放出γ射線。拉賽福和蓋格將<img style="width:40px;" src='https://upload.wikimedia.org/wikipedia/commons/8/80/%E4%BA%9E%E4%BD%9B%E5%8A%A0%E5%8E%A5%E6%95%B8-7.png'/>從暴露在大量<img style="width:30px;" src='https://upload.wikimedia.org/wikipedia/commons/7/77/%E4%BA%9E%E4%BD%9B%E5%8A%A0%E5%8E%A5%E6%95%B8-8.png'/> 數小時之後的固體移開,靜置十五分鐘之後<img style="width:40px;" src='https://upload.wikimedia.org/wikipedia/commons/8/80/%E4%BA%9E%E4%BD%9B%E5%8A%A0%E5%8E%A5%E6%95%B8-7.png'/>幾乎完全衰變,所測得的α粒子幾乎都是從<img style="width:35px;" src='https://upload.wikimedia.org/wikipedia/commons/1/19/%E4%BA%9E%E4%BD%9B%E5%8A%A0%E5%8E%A5%E6%95%B8-9.png'/>的β衰變後立即由<img style="width:40px;" src='https://upload.wikimedia.org/wikipedia/commons/8/80/%E4%BA%9E%E4%BD%9B%E5%8A%A0%E5%8E%A5%E6%95%B8-7.png'/>產生。實驗測量10分鐘內衰變的α粒子數,並同時在上圖的垂直方向以另一個相似的偵測器測量樣品的γ射線強度。儀器只能量到能量較高的γ射線,由<img style="width:40px;" src='https://upload.wikimedia.org/wikipedia/commons/8/80/%E4%BA%9E%E4%BD%9B%E5%8A%A0%E5%8E%A5%E6%95%B8-7.png'/>產生的γ射線。將測量得到的γ射線強度與處於「放射性平衡」(radioactive equilibrium)的<img style="width:60px;" src='https://upload.wikimedia.org/wikipedia/commons/0/0c/%E4%BA%9E%E4%BD%9B%E5%8A%A0%E5%8E%A5%E6%95%B8-1.png'/>標準品的γ射線強度作比較,推算出樣本的相對<img style="width:60px;" src='https://upload.wikimedia.org/wikipedia/commons/0/0c/%E4%BA%9E%E4%BD%9B%E5%8A%A0%E5%8E%A5%E6%95%B8-1.png'/>質量,再算出每單位時間單位質量釋放的α粒子數。 | ||
| − | ::在拉賽福的時代,<img style="width:35px;" src='https://upload.wikimedia.org/wikipedia/commons/7/77/%E4%BA%9E%E4%BD%9B%E5%8A%A0%E5%8E%A5%E6%95%B8-8.png'/> 稱為”radium emanation”(蒸散後的鐳),<img style="width:40px;" src='https://upload.wikimedia.org/wikipedia/commons/f/fe/%E4%BA%9E%E4%BD%9B%E5%8A%A0%E5%8E%A5%E6%95%B8-10.png'/>、<img style="width:40px;" src='https://upload.wikimedia.org/wikipedia/commons/4/4e/%E4%BA%9E%E4%BD%9B%E5%8A%A0%E5%8E%A5%E6%95%B8-11.png'/>和<img style="width: | + | ::在拉賽福的時代,<img style="width:35px;" src='https://upload.wikimedia.org/wikipedia/commons/7/77/%E4%BA%9E%E4%BD%9B%E5%8A%A0%E5%8E%A5%E6%95%B8-8.png'/> 稱為”radium emanation”(蒸散後的鐳),<img style="width:40px;" src='https://upload.wikimedia.org/wikipedia/commons/f/fe/%E4%BA%9E%E4%BD%9B%E5%8A%A0%E5%8E%A5%E6%95%B8-10.png'/>、<img style="width:40px;" src='https://upload.wikimedia.org/wikipedia/commons/4/4e/%E4%BA%9E%E4%BD%9B%E5%8A%A0%E5%8E%A5%E6%95%B8-11.png'/>和<img style="width:33px;" src='https://upload.wikimedia.org/wikipedia/commons/1/19/%E4%BA%9E%E4%BD%9B%E5%8A%A0%E5%8E%A5%E6%95%B8-9.png'/>分別稱為”radium A”、”radium B”及”radium C”。 |
| − | 讓α射線通過的小孔(D)直徑為1.25 mm,輻射源距離小孔150 cm,10分鐘內偵測器量到45個α粒子,輻射源對應於0.55微克的<img style="width:60px;" src='https://upload.wikimedia.org/wikipedia/commons/0/0c/%E4%BA%9E%E4%BD%9B%E5%8A%A0%E5%8E%A5%E6%95%B8-1.png'/>。 | + | ::讓α射線通過的小孔(D)直徑為1.25 mm,輻射源距離小孔150 cm,10分鐘內偵測器量到45個α粒子,輻射源對應於0.55微克的<img style="width:60px;" src='https://upload.wikimedia.org/wikipedia/commons/0/0c/%E4%BA%9E%E4%BD%9B%E5%8A%A0%E5%8E%A5%E6%95%B8-1.png'/>。 |
*3.2 試將以上拉賽福實驗裝置繪於一圓,並計算出每單位時間單位質量釋放的α粒子數(參考答案如式[2]所示) | *3.2 試將以上拉賽福實驗裝置繪於一圓,並計算出每單位時間單位質量釋放的α粒子數(參考答案如式[2]所示) | ||
| − | + | ::::::::::::::<img style="width:500px;" src='https://upload.wikimedia.org/wikipedia/commons/7/7c/%E4%BA%9E%E4%BD%9B%E5%8A%A0%E5%8E%A5%E6%95%B8-12.png'/> | |
| + | *3.3 閱讀關於拉賽福的實驗之說明 (從鐳生產氦): | ||
| + | ::利用前述的電流訊號放大偵測法,拉賽福等人於1911年以γ射線強度測得實驗中鐳的質量為0.192 mg,經過83天後共產生6.58 mm3的氦,經過132天後共產生10.38 m3的氦(1 atm, 0℃ )。 | ||
| + | ::從<img style="width:60px;" src='https://upload.wikimedia.org/wikipedia/commons/0/0c/%E4%BA%9E%E4%BD%9B%E5%8A%A0%E5%8E%A5%E6%95%B8-1.png'/>衰變到比較穩定的<img style="width:50px;" src='https://upload.wikimedia.org/wikipedia/commons/2/28/%E4%BA%9E%E4%BD%9B%E5%8A%A0%E5%8E%A5%E6%95%B8-6.png'/>過程中,共有4個反應會放出α粒子,和α粒子實驗不同的是,實驗以鐳的鹽類(RaBr2)進行,因此表一所列的其他放射性物質的濃度為零。以實驗時間132天來看,表一中的第三和第四個α粒子輻射反應可以視為處於放射性平衡,第一個α粒子輻射反應極為緩慢,其反應速率可視為常數。若每天由<img style="width:60px;" src='https://upload.wikimedia.org/wikipedia/commons/0/0c/%E4%BA%9E%E4%BD%9B%E5%8A%A0%E5%8E%A5%E6%95%B8-1.png'/>釋放的α粒子所產生的氦氣體積為x,則其他三個α粒子輻射反應所產生的氦氣體積應小於y = 3x。在反應的第T天,氦氣的體積如式[3]所示: | ||
| + | ::::::::::::::<img style="width:400px;" src='https://upload.wikimedia.org/wikipedia/commons/a/ae/%E4%BA%9E%E4%BD%9B%E5%8A%A0%E5%8E%A5%E6%95%B8-13.png | ||
| + | '/> | ||
| + | ::在式[3]中的第一項是由<img style="width:60px;" src='https://upload.wikimedia.org/wikipedia/commons/0/0c/%E4%BA%9E%E4%BD%9B%E5%8A%A0%E5%8E%A5%E6%95%B8-1.png'/>產生的的氦氣體積,第二項是<img style="width:30px;" src='https://upload.wikimedia.org/wikipedia/commons/7/77/%E4%BA%9E%E4%BD%9B%E5%8A%A0%E5%8E%A5%E6%95%B8-8.png'/>每天α粒子輻射產生氦氣的三倍體積,積分式[3]得,<img style="width:20px;" src='https://upload.wikimedia.org/wikipedia/commons/3/3e/%E4%BA%9E%E4%BD%9B%E5%8A%A0%E5%8E%A5%E6%95%B8-14.png'/>是<img style="width:60px;" src='https://upload.wikimedia.org/wikipedia/commons/0/0c/%E4%BA%9E%E4%BD%9B%E5%8A%A0%E5%8E%A5%E6%95%B8-1.png'/>的α衰變速率常數,因為<img style="width:100px;" src='https://upload.wikimedia.org/wikipedia/commons/1/18/%E4%BA%9E%E4%BD%9B%E5%8A%A0%E5%8E%A5%E6%95%B8-15.png'/>,以實驗的天數,積分中的<img style="width:25px;" src='https://upload.wikimedia.org/wikipedia/commons/0/06/%E4%BA%9E%E4%BD%9B%E5%8A%A0%E5%8E%A5%E6%95%B8-16.png'/>趨近於零,因此式[3]可以近似,如式[4]所示: | ||
| + | ::::::::::::::<img style="width:400px;" src='https://upload.wikimedia.org/wikipedia/commons/1/1a/%E4%BA%9E%E4%BD%9B%E5%8A%A0%E5%8E%A5%E6%95%B8-17.png'/> | ||
| + | ::將83 d 和132 d帶入分別得到3.801x和3.875x,也就是應得的氦氣體積和x的倍數關係。以83d數據計算,得式[5]。 | ||
| + | ::::::::::::::<img style="width:400px;" src='https://upload.wikimedia.org/wikipedia/commons/f/ff/%E4%BA%9E%E4%BD%9B%E5%8A%A0%E5%8E%A5%E6%95%B8-18.png'/> | ||
| + | ::以132 d數據計算,得式[6]。 | ||
| + | ::::::::::::::<img style="width:400px;" src='https://upload.wikimedia.org/wikipedia/commons/b/b3/%E4%BA%9E%E4%BD%9B%E5%8A%A0%E5%8E%A5%E6%95%B8-19.png'/> | ||
| + | ::取其平均 。將 除以0.192 g,得到每公克<img style="width:60px;" src='https://upload.wikimedia.org/wikipedia/commons/0/0c/%E4%BA%9E%E4%BD%9B%E5%8A%A0%E5%8E%A5%E6%95%B8-1.png'/>每天產生的氦氣體積,如式[7]所示: | ||
| + | ::::::::::::::<img style="width:400px;" src='https://upload.wikimedia.org/wikipedia/commons/7/7e/%E4%BA%9E%E4%BD%9B%E5%8A%A0%E5%8E%A5%E6%95%B8-20.png'/> | ||
| + | *3.4 試從兩個實驗數據計算出亞佛加爵常數,查詢常數之準確值,以你的數值和準確值比較。你認為你所得的數值準確度如何? 造成計算誤差的可能原因為何? | ||
| + | <br><br> | ||
| + | ==分析與結論 == | ||
| + | 利用1908和1911年的兩組拉賽福實驗數據,從α粒子實驗得到的<img style="width:60px;" src='https://upload.wikimedia.org/wikipedia/commons/0/0c/%E4%BA%9E%E4%BD%9B%E5%8A%A0%E5%8E%A5%E6%95%B8-1.png'/>的α衰變速率為<img style="width:100px;" src='https://upload.wikimedia.org/wikipedia/commons/7/7a/%E4%BA%9E%E4%BD%9B%E5%8A%A0%E5%8E%A5%E6%95%B8-21.png'/>,從氦氣實驗得到<img style="width:60px;" src='https://upload.wikimedia.org/wikipedia/commons/0/0c/%E4%BA%9E%E4%BD%9B%E5%8A%A0%E5%8E%A5%E6%95%B8-1.png'/>的α衰變產生氦氣的速率為<img style="width:120px;" src='https://upload.wikimedia.org/wikipedia/commons/0/0e/%E4%BA%9E%E4%BD%9B%E5%8A%A0%E5%8E%A5%E6%95%B8-22.png'/>。 | ||
| + | (此處d為day的縮寫,1 d = 86400 seconds) | ||
| + | 由於在0 ℃且一大氣壓下氣體的莫耳體積是22.4 L,因此利用以上兩個數據透過等式計算,可得亞佛加厥常數<img style="width:50px;" src='https://upload.wikimedia.org/wikipedia/commons/6/6b/%E4%BA%9E%E4%BD%9B%E5%8A%A0%E5%8E%A5%E6%95%B8-3.png'/>,如式[1]所示: | ||
| + | :::::<img style="width:500px;" src='https://upload.wikimedia.org/wikipedia/commons/b/b9/%E4%BA%9E%E4%BD%9B%E5%8A%A0%E5%8E%A5%E6%95%B8-23.png'/> | ||
| + | |||
| + | 由式[1]可得到<img style="width:150px;" src='https://upload.wikimedia.org/wikipedia/commons/5/5a/%E4%BA%9E%E4%BD%9B%E5%8A%A0%E5%8E%A5%E6%95%B8-24.png'/> | ||
| + | 利用1908和1911年兩組實驗數據,得到的亞佛加厥常數與準確值<img style="width:150px;" src='https://upload.wikimedia.org/wikipedia/commons/7/7a/%E4%BA%9E%E4%BD%9B%E5%8A%A0%E5%8E%A5%E6%95%B8-2.png'/> 差異不大。 | ||
<br><br> | <br><br> | ||
| − | == | + | ==教學目標與評量 == |
| − | * | + | *5.1 了解亞佛加厥常數 |
| − | + | *5.2 了解「鐳-226輻射α粒子的速率」與「從鐳生產氦」兩組實驗的內容 | |
| − | + | *5.3 學習如何結合兩組實驗數據推得亞佛加厥常數 | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
<br><br> | <br><br> | ||
| − | == | + | ==參考資料 == |
*6.1 參考文獻 | *6.1 參考文獻 | ||
| − | ::[1] | + | ::[1] Avogadro constant, https://en.wikipedia.org/wiki/Avogadro_constant. |
| − | ::[2] | + | ::[2] Rutherford, E.; Geiger, H. Proc. R. Soc. Lond. A 1908, 81, 162-173. |
| − | + | ::[3] Boltwood, B. B.; Rutherford, E. Philos. Mag. 1911, 22, 586-604. | |
| − | : | + | ::[4] Leenson, I. A. J. Chem. Edu. 1998, 75, 998-1003 |
| − | + | ||
| − | |||
| − | :: | ||
<br><br><br><br><br><br><br> | <br><br><br><br><br><br><br> | ||
於 2020年8月5日 (三) 02:45 的最新修訂
原始設計者:彰師大
|
介紹二十世紀初利用兩組拉賽福(Ernest Rutherford, 1871 – 1937)的實驗數據,分別是在1908年的α射線的鐳-226
|
|
現象說明
亞佛加厥常數
 的準確數值為
的準確數值為
 ,
12公克的碳-12含有
,
12公克的碳-12含有
 個碳原子。雖然
個碳原子。雖然
 的數值對於化學家至為重要,但是其準確值的獲得是相當近代的事。一個世紀以前的科學家們在準確度偏低的測量數據中,是如何推演出亞佛加厥常數的呢?
的數值對於化學家至為重要,但是其準確值的獲得是相當近代的事。一個世紀以前的科學家們在準確度偏低的測量數據中,是如何推演出亞佛加厥常數的呢?
探究問題
- 2.1 亞佛加厥常數的計算方法。
- 2.2 根據實驗「鐳-226輻射α粒子的速率」與「從鐳生產氦」所得數據計算亞佛加厥常數。
- 2.3 比較實驗所推得的亞佛加厥常數與準確值。
實作項目
- 3.1 閱讀關於拉賽福的實驗之說明
- 鐳-226輻射α粒子的速率:
- 在1908年,拉賽福和蓋格(Johannes Wilhelm "Hans" Geiger, 1882 – 1945)發表
 輻射α粒子的速率,他們的實驗裝置如圖一所示:
輻射α粒子的速率,他們的實驗裝置如圖一所示:
- 圖一之右是偵測器(detecting vessel),抽氣至低壓(2-5 cm Hg)。A是包覆於電池正極的管柱,B是一條連到電池負極的電線,外加電壓。被α粒子游離的氣體,會將電流訊號放大數千倍傳到B為硬橡皮塞,D是讓α射線通過的小孔,直徑為數毫米,孔上裝有薄雲母片(將α粒子減速)。E為長玻璃管,輻射源可放置在距C不同長度的位置。F是活塞活栓,打開後α粒子可穿透到偵測器,G是磨口玻璃塞。
- 我們將鐳-226
 的主要衰變路徑及其半衰期列於表一。
的主要衰變路徑及其半衰期列於表一。

- (資料來源:https://en.wikipedia.org/wiki/Radium)
- 表一 的主要衰變路徑及其半衰期
- (資料來源:https://en.wikipedia.org/wiki/Radium)
- 從鐳-226
 衰變到比較穩定的鉛-210
衰變到比較穩定的鉛-210 過程中,共有4個反應會放出α粒子,有3個反應會放出γ射線。拉賽福和蓋格將
過程中,共有4個反應會放出α粒子,有3個反應會放出γ射線。拉賽福和蓋格將 從暴露在大量
從暴露在大量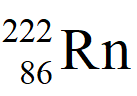 數小時之後的固體移開,靜置十五分鐘之後
數小時之後的固體移開,靜置十五分鐘之後 幾乎完全衰變,所測得的α粒子幾乎都是從
幾乎完全衰變,所測得的α粒子幾乎都是從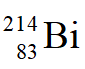 的β衰變後立即由
的β衰變後立即由 產生。實驗測量10分鐘內衰變的α粒子數,並同時在上圖的垂直方向以另一個相似的偵測器測量樣品的γ射線強度。儀器只能量到能量較高的γ射線,由
產生。實驗測量10分鐘內衰變的α粒子數,並同時在上圖的垂直方向以另一個相似的偵測器測量樣品的γ射線強度。儀器只能量到能量較高的γ射線,由 產生的γ射線。將測量得到的γ射線強度與處於「放射性平衡」(radioactive equilibrium)的
產生的γ射線。將測量得到的γ射線強度與處於「放射性平衡」(radioactive equilibrium)的 標準品的γ射線強度作比較,推算出樣本的相對
標準品的γ射線強度作比較,推算出樣本的相對 質量,再算出每單位時間單位質量釋放的α粒子數。
質量,再算出每單位時間單位質量釋放的α粒子數。 - 在拉賽福的時代,
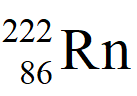 稱為”radium emanation”(蒸散後的鐳),
稱為”radium emanation”(蒸散後的鐳),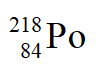 、
、 和
和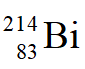 分別稱為”radium A”、”radium B”及”radium C”。
分別稱為”radium A”、”radium B”及”radium C”。 - 讓α射線通過的小孔(D)直徑為1.25 mm,輻射源距離小孔150 cm,10分鐘內偵測器量到45個α粒子,輻射源對應於0.55微克的
 。
。
- 3.2 試將以上拉賽福實驗裝置繪於一圓,並計算出每單位時間單位質量釋放的α粒子數(參考答案如式[2]所示)
- 3.3 閱讀關於拉賽福的實驗之說明 (從鐳生產氦):
- 利用前述的電流訊號放大偵測法,拉賽福等人於1911年以γ射線強度測得實驗中鐳的質量為0.192 mg,經過83天後共產生6.58 mm3的氦,經過132天後共產生10.38 m3的氦(1 atm, 0℃ )。
- 從
 衰變到比較穩定的
衰變到比較穩定的 過程中,共有4個反應會放出α粒子,和α粒子實驗不同的是,實驗以鐳的鹽類(RaBr2)進行,因此表一所列的其他放射性物質的濃度為零。以實驗時間132天來看,表一中的第三和第四個α粒子輻射反應可以視為處於放射性平衡,第一個α粒子輻射反應極為緩慢,其反應速率可視為常數。若每天由
過程中,共有4個反應會放出α粒子,和α粒子實驗不同的是,實驗以鐳的鹽類(RaBr2)進行,因此表一所列的其他放射性物質的濃度為零。以實驗時間132天來看,表一中的第三和第四個α粒子輻射反應可以視為處於放射性平衡,第一個α粒子輻射反應極為緩慢,其反應速率可視為常數。若每天由 釋放的α粒子所產生的氦氣體積為x,則其他三個α粒子輻射反應所產生的氦氣體積應小於y = 3x。在反應的第T天,氦氣的體積如式[3]所示:
釋放的α粒子所產生的氦氣體積為x,則其他三個α粒子輻射反應所產生的氦氣體積應小於y = 3x。在反應的第T天,氦氣的體積如式[3]所示:
- 在式[3]中的第一項是由
 產生的的氦氣體積,第二項是
產生的的氦氣體積,第二項是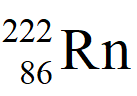 每天α粒子輻射產生氦氣的三倍體積,積分式[3]得,
每天α粒子輻射產生氦氣的三倍體積,積分式[3]得, 是
是 的α衰變速率常數,因為
的α衰變速率常數,因為 ,以實驗的天數,積分中的
,以實驗的天數,積分中的 趨近於零,因此式[3]可以近似,如式[4]所示:
趨近於零,因此式[3]可以近似,如式[4]所示:
- 將83 d 和132 d帶入分別得到3.801x和3.875x,也就是應得的氦氣體積和x的倍數關係。以83d數據計算,得式[5]。
- 以132 d數據計算,得式[6]。
- 取其平均 。將 除以0.192 g,得到每公克
 每天產生的氦氣體積,如式[7]所示:
每天產生的氦氣體積,如式[7]所示:
- 3.4 試從兩個實驗數據計算出亞佛加爵常數,查詢常數之準確值,以你的數值和準確值比較。你認為你所得的數值準確度如何? 造成計算誤差的可能原因為何?
分析與結論
利用1908和1911年的兩組拉賽福實驗數據,從α粒子實驗得到的 的α衰變速率為
的α衰變速率為 ,從氦氣實驗得到
,從氦氣實驗得到 的α衰變產生氦氣的速率為
的α衰變產生氦氣的速率為 。
(此處d為day的縮寫,1 d = 86400 seconds)
由於在0 ℃且一大氣壓下氣體的莫耳體積是22.4 L,因此利用以上兩個數據透過等式計算,可得亞佛加厥常數
。
(此處d為day的縮寫,1 d = 86400 seconds)
由於在0 ℃且一大氣壓下氣體的莫耳體積是22.4 L,因此利用以上兩個數據透過等式計算,可得亞佛加厥常數 ,如式[1]所示:
,如式[1]所示:
由式[1]可得到 利用1908和1911年兩組實驗數據,得到的亞佛加厥常數與準確值
利用1908和1911年兩組實驗數據,得到的亞佛加厥常數與準確值 差異不大。
差異不大。
教學目標與評量
- 5.1 了解亞佛加厥常數
- 5.2 了解「鐳-226輻射α粒子的速率」與「從鐳生產氦」兩組實驗的內容
- 5.3 學習如何結合兩組實驗數據推得亞佛加厥常數
參考資料
- 6.1 參考文獻
- [1] Avogadro constant, https://en.wikipedia.org/wiki/Avogadro_constant.
- [2] Rutherford, E.; Geiger, H. Proc. R. Soc. Lond. A 1908, 81, 162-173.
- [3] Boltwood, B. B.; Rutherford, E. Philos. Mag. 1911, 22, 586-604.
- [4] Leenson, I. A. J. Chem. Edu. 1998, 75, 998-1003







